Train-validation split
How do we know if we are overfitting or underfitting? Note that we do not have access to the ground truth function \(f\) (otherwise there is no point in doing ML) or the expected model \(\bar{f}\) (too expensive to estimate). How do we select algorithm or hyperparameters? This can be done simply by reserving a subset of the dataset called the validation set for estimating the true risk. The validation performance is used for choosing hyperparameters and tweaking the model class. Recall that the training dataset is used to minimize the empirical risk. In terms of train and validation loss:
Overfitting is characterized by significant \(\mathcal{L}_{\mathcal{D}_{\text{train}}}(\boldsymbol{\Theta}) \ll \mathcal{L}_{\mathcal{D}_{\text{val}}}(\boldsymbol{\Theta})\).
Underfitting is characterized by \(\mathcal{L}_{\mathcal{D}_{\text{train}}}(\boldsymbol{\Theta})\) not decreasing low enough (Fig. 14).
The training and validation curves are generated by \((t, \mathcal{L}_{\mathcal{D}_{\text{train}}}(\boldsymbol{\Theta}^t))\) and \((t, \mathcal{L}_{\mathcal{D}_{\text{val}}}(\boldsymbol{\Theta}^t))\) for steps \(t\) during training (Fig. 14). The model only sees the train set during training. Meanwhile, the model is evaluated on the same validation set getting controlled results. Note that modifying training hyperparameters between runs means that the validation set is now being overfitted. Techniques such as k-fold cross-validation or mitigates this, but can be expensive for training large models. Training ends with a final set of parameters \(\hat{\boldsymbol{\Theta}}.\)
Finally, a separate test set is used to report the final performance. The loss on the test set \(\mathcal{L}_{\mathcal{D}_{\text{test}}}(\hat{\boldsymbol{\Theta}})\) acts as the final estimate of the true risk of the trained model. It is best practice that the test evaluation is done exactly once. Note that the training, validation, and test sets are chosen to be disjoint.
Remarks. Regularization tends to flatten out the classical U-shape validation curve that occurs before epoch-wise double descent (Fig. 10) where the model overfits. Assuming the model is sufficiently complex so that there is little bias, underfitting can indicate a problem with the optimizer (e.g. learning rate). We will see in the next chapter that training loss curves stuck to values away from zero may indicate a problem with the optimizer (stuck in a plateau, or bad local optima).
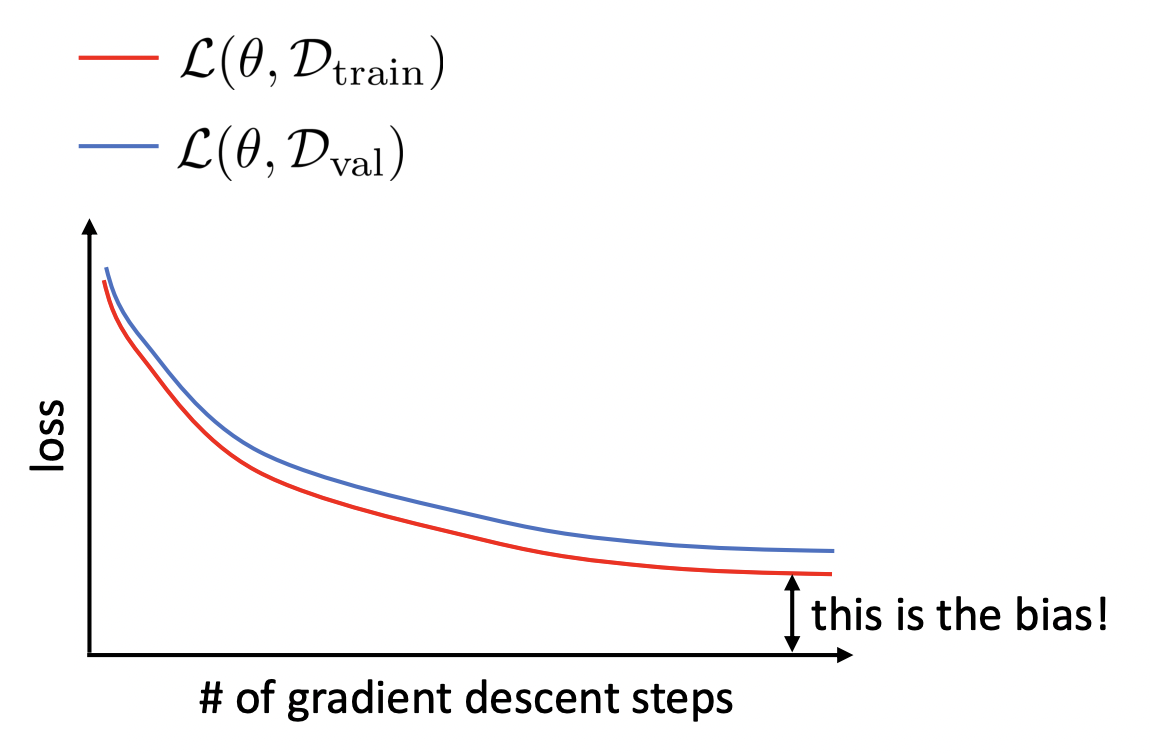
Fig. 14 Train and validation loss curves during training. Gap in train curve can indicate bias or a problem with the optimizer. Source: [CS182-lec3]
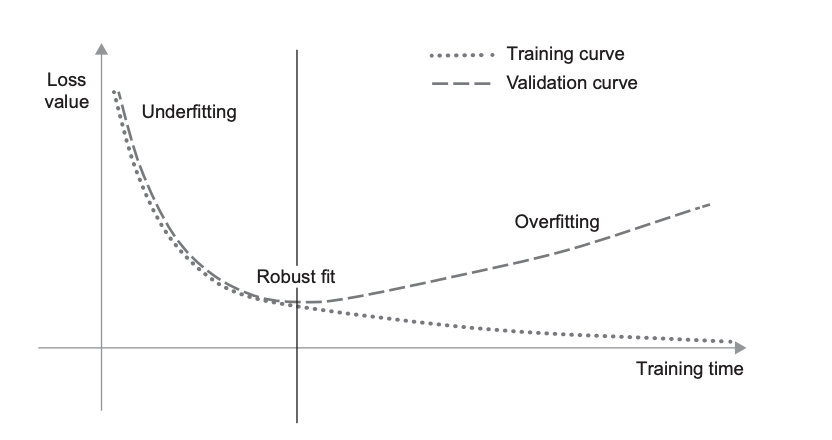
Fig. 15 Canonical train-validation loss curves. Source: [Cho21]
Remark. A commonly used technique is early stopping which stops training once the validation curves stops improving after a set number of steps. One consequence of epoch-wise double descent is that early stopping only helps in the relatively narrow parameter regime of critically parameterized models (Fig. 10)! In fact, practical experience shows that early stopping results in overfitting the validation set (Fig. 16).

Fig. 16 Top Kaggle GMs recommending against the use of early stopping. Source: [video]